【FP2級】ライフプランニングと６つの係数〜係数は３セットで整理しよう！〜

＊このページは2020年4月19日に更新しました。

ライフプランニング

ライフプランニングとは

ライフプランとは「人生設計」のこと。

つまり、ライフプランニングとは「人生設計をすること」を指します。

人生には就職、結婚、子育て、住宅の購入などなど、様々なライフイベントが発生します。

ライフイベントによっては多大なお金がかかるわけですから、あらかじめライフイベントを予測して計画的にお金の準備をすることが大切であり、そのアドバイスを行うのがFPの重要な仕事の一つです。

具体的なライフプランニングのやり方として、まずは顧客の属性やヒアリングなどを通じてライフイベント表やキャッシュフロー表を作成していきます。

キャッシュフロー表とは、未来のライフイベントに向けた資金計画を表にしたものです。

現在の貯蓄を運用したり、年間の収支を積み重ねて、数年後にいくらのお金が準備できるかといったことを整理していきます。

可処分所得とは

キャッシュフロー表を作成する際におさえておきたいのが「可処分所得」の定義です。

給与所得者の方なら分かると思いますが、額面の給与が全て口座に入金されるわけではありません。

実際に手元に入るのは、税金（所得税・住民税）や社会保険料が差し引かれた金額になりますよね。

この実際に手元に残った所得を「可処分所得」と呼び、FP２級では計算問題が出されることがあります。

可処分所得を算出するための定義はしっかりおさえておきましょう。

６つの係数とは

６つの係数をマスターしよう

キャッシュフロー表をつくるに当たっては、例えば「今ある100万円を年２％で運用すると５年後にはいくらになっているか？」とか、「10年後の学費を準備するために毎年いくら積立てれば良いか？」といったことを計算する必要が出てきます。

こういった計算を簡単に行うために用いるのが次の６つの係数です。

元となる金額に目的に応じた係数を乗じることで、求めたい金額を算出します。

【元本運用系】終価係数と現価係数

まずは、「終価係数」と「現価係数」です。

この２つはセットで覚えておきましょう。

終価係数は「元本を複利で運用すると、将来いくらになるかを求めるとき」に、現価係数は「将来の目標金額を達成するために、必要な元本を求めるとき」に使う係数でしたね。

どちらも元本がキーワードになるので、この２つを「元本運用系」と名付けます。

「元本」とは、要するに元手（もとで）のことです。

式で表すと次のようになります。

まだちょっとイメージが湧きませんね。

練習問題を見てみましょう。

先ほどの式に当てはめると答えは簡単です。

100万円×1.3439（3%・10年の終価係数）＝1,343,900円

100万円の元本を毎年３％の複利で運用すれば、10年後には1,343,900円になるということですね。

今度は「現価係数」を使う練習問題を見てみましょう。

こちらも式に当てはめれば簡単ですね。

100万円×0.7441（3%・10年の現価係数）＝744,100円

年３％の複利で運用し、10年後に100万円を手に入れるためには、744,100円の元本が必要だということです。

終価係数と現価係数の関係を図にすると次のようなイメージです。

 

 

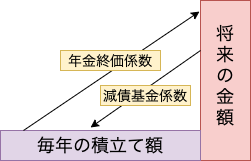
【積立系】年金終価係数と減債基金係数

次に「年金終価係数」と「減債基金係数」を学習します。

この２つもセットで覚えておきましょう。

年金終価係数は「毎年一定額の積立てをした場合に、将来いくらになるかを求めるとき」に、減債基金係数は「将来の目標積立て金額を達成するために、毎年いくら積み立ればよいかを求めるとき」に使う係数でしたね。

どちらも積立てがキーワードになるので、この２つを「積立系」と名付けます。

「積立系」の２つを式で表すと次のようになります。

今回もイメージが湧くように練習問題を見てみましょう。

年金終価係数の式に当てはめると次のようになります。

10万円×10.950（２%・10年の年金終価係数）＝1,095,000円

難しくありませんね。

毎年10万円ずつ積立て、2％の複利で運用すれば、10年後には1,095,000円になっているということです。

次は「減債基金係数」を使う練習問題を見てみましょう。

減債基金係数の式に当てはめると次のようになります。

100万円×0.0913（2%・10年の減債基金係数）＝ 91,300円

10年後に100万円貯蓄するためには、毎年91,300円ずつ積立て年2％で運用すればよいということになります。

終価係数と現価係数の関係を図にすると次のようなイメージです。

 

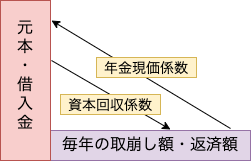
【取崩し・返済系】年金現価係数と資本回収係数

最後に、「年金現価係数」と「資本回収係数」のセットです。

ここが少し難しいので、できるだけ分かりやすく解説していきます。

まず、年金現価係数は「毎年一定金額を受け取るために必要な元本を求めるとき」と「年間の返済金額から借入金の総額を求めるとき」に使う係数でした。

資本回収係数の方は、「元本を取り崩して毎年受け取れる金額を求めるとき」と「借入金の総額から年間の返済金額を求めるとき」に使う係数でしたね。

この２つを「取崩し・返済系」と名付けます。

式で表すと次のようになります。

ちょっとややこしいですね。

そんな時は実際に問題を解いてみるのが理解への近道です。

毎年一定金額を受け取るために必要な元本を求めるので、年金現価係数を使って計算をします。

100万円×8.983（2%・10年の年金現価係数）＝ 8,983,000円

例えば、70歳から80歳にかけて毎年100万円（合計1,000万円）を受取りたいのであれば、8,983,000円を用意して、受け取った金額の残りを２％で運用すればよいということですね。

仮に「年２％の借入金利で年間100万円ずつ返済する場合の借入金の総額はいくらになるでしょう？」という問題だったとしても、答えは全く同じになります。

問題文に惑わされないようにしましょうね。

今度は資本回収係数の練習問題を見ていきます。あと一息です。

元本を取崩して毎年受け取れる金額を求めるので、資本回収係数を使います。

1,000万円×0.11133（2%・10年の資本回収係数）＝1,113,300円

元本1,000万円を年２％で複利運用すれば、1,113,300円を10年間受け取れるということです。

最後にもう１つだけ練習問題を見てみましょう。

FP２級対策としてはぜひとも押さえておきたい問題です。

借入金の総額から年間の返済金額を求めるので、資本回収係数を使います。

お気づきかもしれませんが、練習問題(6)と全く同じ計算になります。

1,000万円×0.11133（2%・10年の資本回収係数）＝1,113,300円

1,000万円を金利2％で借りた場合、10年で返済するためには毎年1,113,300円ずつ返済していく必要があるということですね。

年金現価係数と資本回収係数の関係を図にすると次のようなイメージです。

 

６つの係数のまとめ

最後に６つの係数を改めて整理しておきましょう。

６つ覚えるというより、３組として覚えておくと分かりやすいです。

元本運用系

積立系

取崩し・返済系

＞＞住宅資金